P2M: A Fast Solver for Querying Distance from Point to Mesh Surface

Abstract

Most of the prevailing point-to-mesh distance query solvers, such as Proximity Query Package (PQP)[Larsen et al.1999], Embree[Afra et al.2016] and Fast Closest Point Query (FCPW)[Sawhney 2021], are based on bounding volume hierarchy (BVH). The hierarchical organizational structure enables one to eliminate the vast majority of triangles that do not help find the closest point. In this paper, we develop a totally different algorithmic paradigm, named P2M, to speed up point-to-mesh distance queries. Our original intention is to precompute a KD tree (KDT) of mesh vertices to approximately encode the geometry of a mesh surface containing vertices, edges and faces. However, it is very likely that the closest primitive to the query point is an edge (resp., a face), but the KDT reports a mesh vertex instead. We call this mesh vertex an interceptor of the edge (resp., a face). The main contribution of this paper is to invent a simple yet effective interception inspection rule and an efficient flooding interception inspection algorithm for quickly finding out all the interception pairs. Once the KDT and the interception table are precomputed, the query stage proceeds by first searching the KDT and then looking up the interception table to retrieve the closest geometric primitive. Statistics show that our query algorithm runs many times faster than the state-of-the-art solvers.

Introduction

To efficiently precompute the interception table, we suggest two techniques for fast interception inspection. First,relaxing the intersection domain between cells into a convex polytope and use an effective filtering rule for fast interception inspection. Second, we suggest a flooding procedure of interception inspection to avoid exhausting all the vertex-edge and vertex-face pairs. These techniques are simple yet effective and enable to precompute the interception table in a short period of time. In fact, the pre-processing time for the interception table is about two minutes for a 1500K-face model, compared to more than one day for a brute-force approach.
Overall, our method aims to improve the query speed for a wide range of research fields that require fast query of the closest geometric primitive on a mesh surface, including computer graphics, physical simulation, computational geometry, and computer-aided design.

Results

Different vertices have different numbers of intercepted primitives.We visualize the vertices in varying colors according to the length of inter- ception list. We set the vertical axis to be in a logarithmic scale. The vertexcolored in red owns a long interception list.

Cost breakdown of query performance on 5 models.

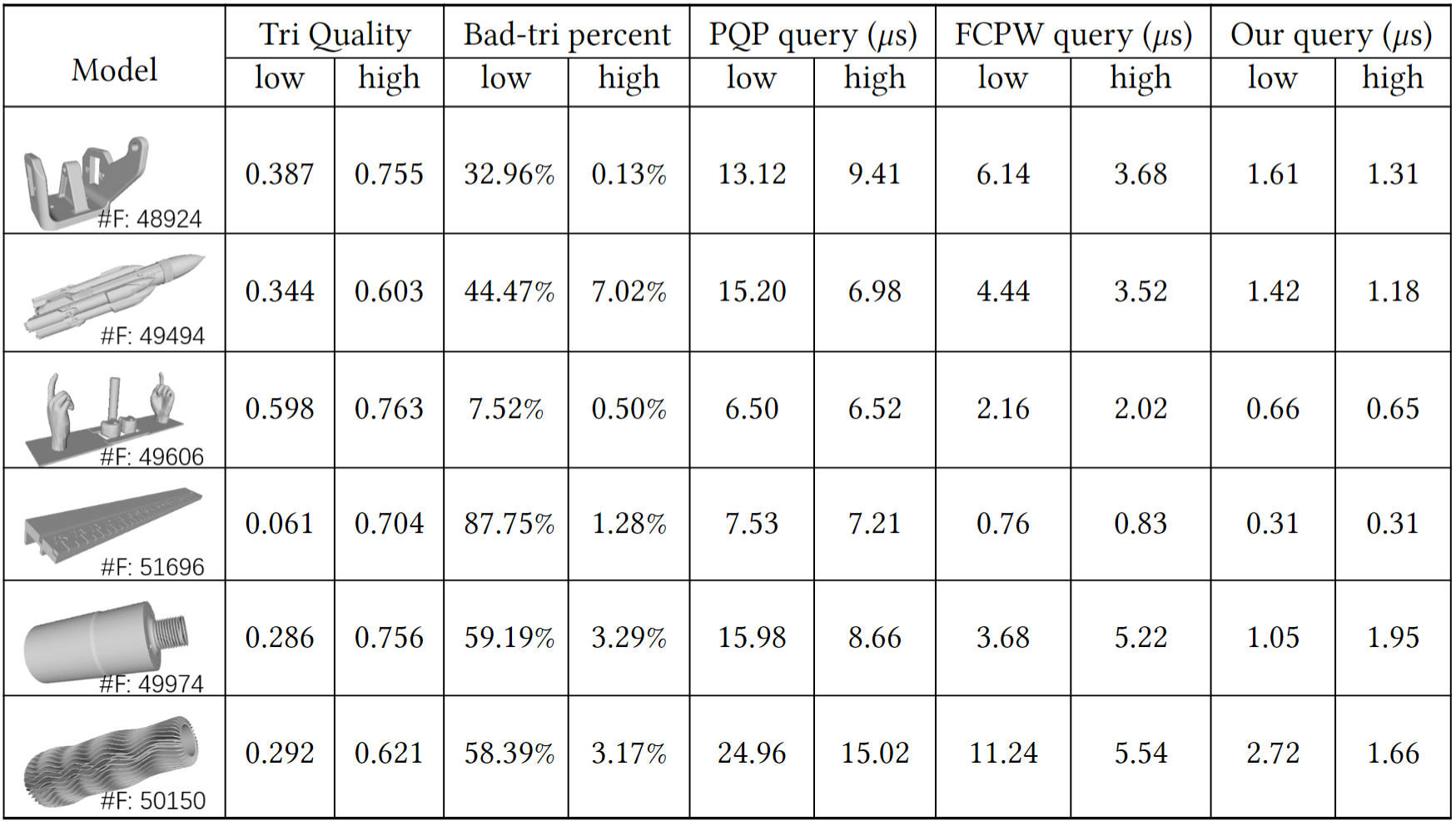
Our method achieves good query efficiency on both high and low quality meshes. Each of the six models has a low quality triangle mesh, and a high quality counterpart. The high quality counterparts of the We list the PQP, FCPW, and our query efficiency on these test models. and our query performance on these test models

Test PQP, FCPW and ours on the Bear model with water-tight/broken triangulation. (left) Watertight triangulation. (center) Triangle soup with gapped triangles. (right) Triangle soup with high penetration. Our comparative advantage over BVH-based methods becomes smaller for a set of gapped triangles whereas larger in the presence of high penetration.

We have tested the query efficiency on the complete Thingi10K dataset[Zhou and Jacobson 2016], which is a comparison of the query efficiency of PQP,FCPW and our method on Thingi10K.